<자료구조 알고리즘> 그래프 표현 3. edge list (간선 리스트)

그래프가 무엇인지 모르시는 분들은 아래 글을 참고하길 바랍니다.
https://jjoonleo.tistory.com/11

<자료구조 알고리즘> 그래프 개념

그래프의 표현 방식

이번 글에서는 그래프의 표현 방식에 대해 알아 보도록 하겠다.
그래프는 배열이나 큐 스택과는 다르게 어떻게 구현해야 할지 바로 떠오르지는 않는 것 같다.(나만 그랬나??)
그래프의 표현 방식에는 3가지가 있다.

1. Adjacency List (인접 리스트)
2. Adjacency matrix (인접 행렬)
3. edge list (간선 리스트)

 

3. Edge List

edge list는 그래프의 모든 간선을 piar<int,int>형 일차원 배열에 저장한다.

정점x에서 y로 가는 간선이 존재한다면 배열에 (x,y)를 저장한다. 

이 역시 간선들의 순서는 중요하지 않다.

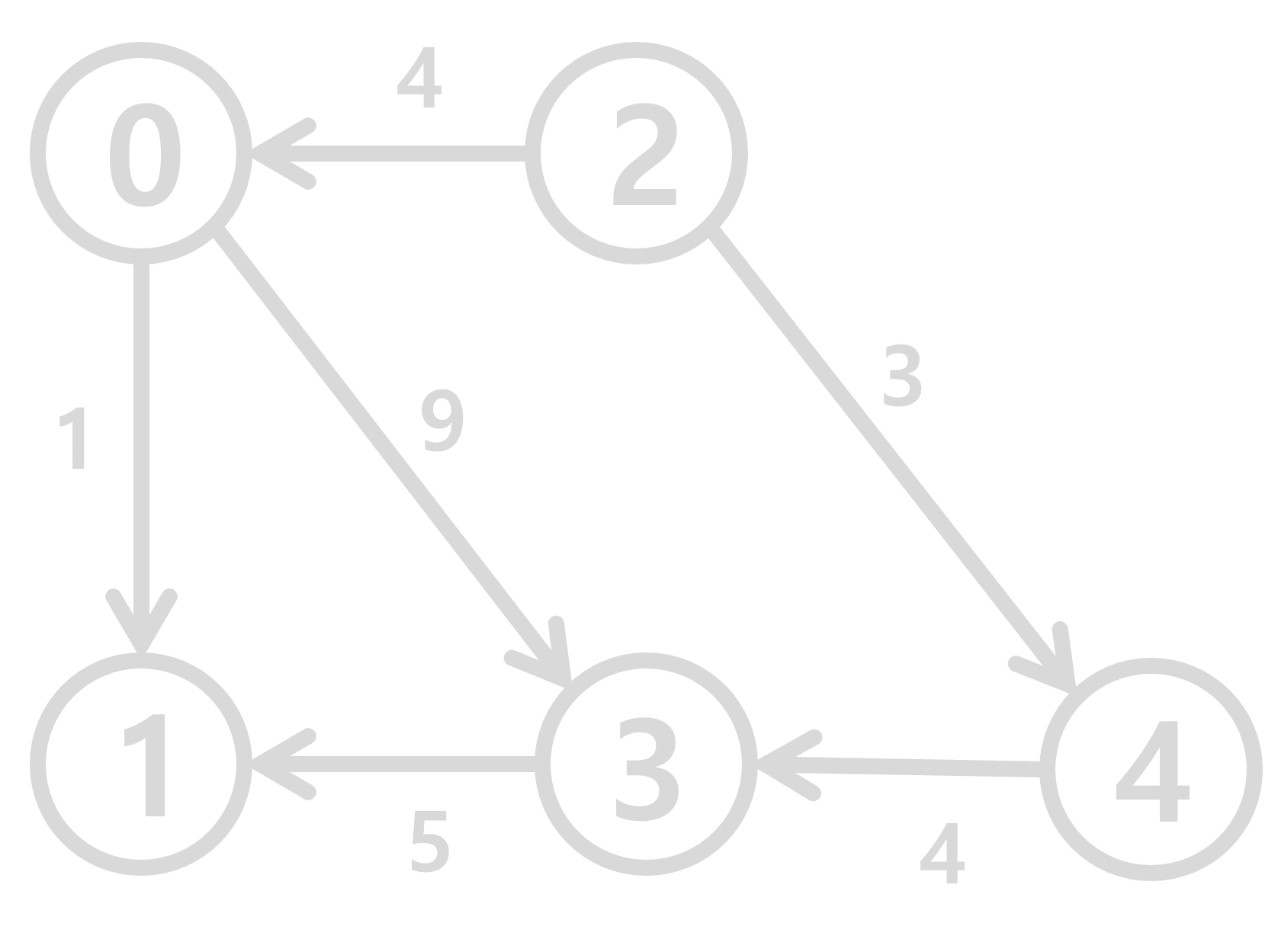
위의 그래프를 edge list로 나타낸다면 다음과 같을 것이다.

0	1
0	3
2	0
2	4
3	1
4	3

이는 일차원 벡터를 이용해서 구현할 수 있다. 

vector<pair<int,int>> edges;

edges.push_back(make_pair(0,1));
edges.push_back(make_pair(0,3));
edges.push_back(make_pair(2,0));
edges.push_back(make_pair(2,4));
edges.push_back(make_pair(3,1));
edges.push_back(make_pair(4,3));

무방향 그래프

그래프가 무방향 그래프라면 양쪽 모두로 방향이 있다고 생각하고 xy를 바꿔서 두 번 씩 저장해도 되지만 효율적으로 간선 당 한 번 씩만 저장하고 처리할 때 고려해서 처리 하는 게 훨씬 효율적일 것이다. 정리하면 방향그래프에서는 (x,y)를 x에서 y로 가는 간선이 있다고 처리했지만 무방향 그래프일 때에는 (x,y)를 x,y사이에 간선이 있다, 즉 x에서도 y로 갈 수 있고 y에서도 x로 갈 수 있다고 처리하면 된다. 

가중치 그래프

가중치도 저장해야 하므로 pair형의 일차원 배열에 저장하는 대신 tuple형의 일차원 배열에 저장하면 된다.

정점x에서 y로 가는 가중치가 w인 간선이 존재한다면 배열에 (x,y,w)를 저장한다. 위의 가중치 그래프를 저장하면 다음과 같다.

vector<tuple<int,int,int>> edges;

edges.push_back(make_tuple(0,1,1));
edges.push_back(make_tuple(0,3,9));
edges.push_back(make_tuple(2,0,4));
edges.push_back(make_tuple(2,4,3));
edges.push_back(make_tuple(3,1,5));
edges.push_back(make_tuple(4,3,4));

Edge List의 특징

- 구현이 가장 간단하다.

- 모든 간선을 탐색할 때 유리하다. (예 벨만-포드 알고리즘)

 

- 특정 두 노드가 이웃한지 알아보려면 모든 간선을 탐색해야 한다.

- 특정 노드에 연결된 간선을 알아보려면 모든 간선을 탐색해야 한다.