※ 이 글은 배열을 처음 배우시는 분들을 위한 글이 아닙니다.
배열이란?
번호(인덱스)와 번호에 대응하는 데이터들로 이루어진 자료구조

그냥 맨날 쓰는 그 배열 맞다. 근데 이 배열에도 종류가 있다.
그리고 그 종류에 따라 각 연산을 하는데 걸리는 시간복잡도가 달라진다.
배열의 종류에 따라 다음 연산에 걸리는 시간복잡도를 계산해 볼 것이다.
- 인덱스가 i인 원소 접근
- i번째에 값 삽입(insertion), 삭제(deletion)
- 마지막에 값 삽입,삭제
- 처음에 값 삽입, 삭제
종류
다음과 같이 분류해 볼 수 있겠다.
1. static array
2. dynamic array
1. Static Array
말 그대로 정적인 배열이다. 즉 한번 할당되고 나면 크기와 길이를 바꿀 수 없는 배열이다.
c언어에서 사용하는 그 int arr[n](n상수)이 static array이다. 저렇게 선언하게 되면 길이 n의 배열이 메모리상에 할당되고 우리는 배열 첫 번째 원소의 주소를 알게 된다.
그럼 각 연산을 하는 방법을 보자
① 인덱스가 i인 원소에 접근
우리가 배열의 첫 번째 원소의주소를 알고 있으니 i번째 원소에 접근하기 위해서는
첫 번째 원소의 주소 + (자료형 크기)*i 한 주소에 접근하면 된다
따라서 시간 복잡도는 O(1)

② 마지막에 값 삽입, 삭제
마지막에 값을 삽입하고 싶지만 크기를 변경할 수 없으니 맨 뒤에 집어 넣을 수가 없다. 그렇기 때문에 지금보다 길이가 1 더 긴 배열을 선언하고 원래의 배열을 복사하고 마지막에 새로운 값을 삽입 하면 된다.
배열의 모든 원소를 복사해야 하므로 시간복잡도는 O(n)
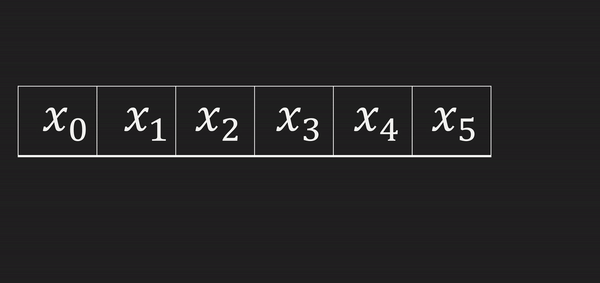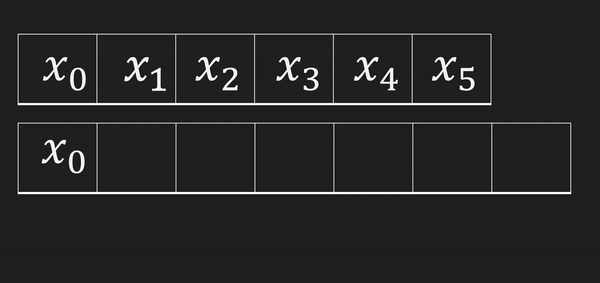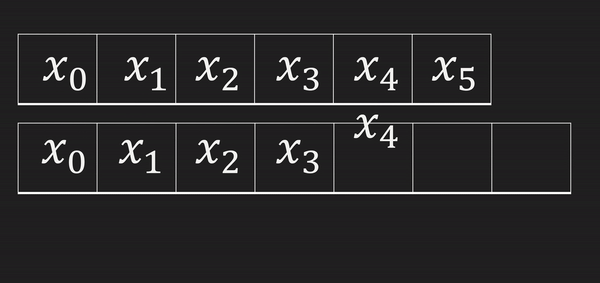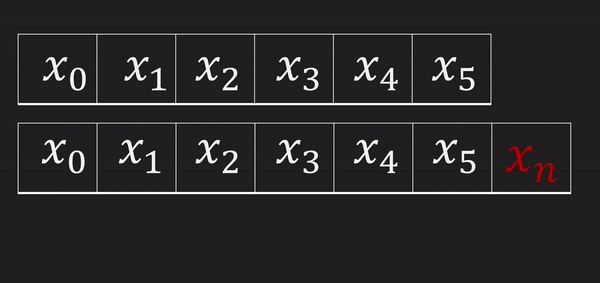
마지막 값을 삭제 하는 것은 값을 없애고 자리를 비워두면 되므로 시간복잡도는 O(1)이다.

③ i번째에 값 삽입, 삭제
위의 방법으로 삽입할 위치를 찾은 후 자리를 확보하기 위해 그 뒤에 오는 원소들을 모두 한 칸씩 뒤로 밀어주면 될 것 같다. 하지만 배열의 크기가 바뀔 수 없으니 자리가 모자라게 된다. 따라서 할 수 없이 새로운 배열 (크기가 지금보다 1큰)을 선언해주고 원소를 복사해주어야 한다.
따라서 시간복잡도는 O(n)

i번째 원소를 삭제하고 나서 그 뒤 모든 원소들을 앞으로 한 칸씩 땡겨서 빈자리를 채워야 한다.
따라서 시간복잡도는 O(n)

④ 처음에 값 삽입, 삭제
이것도 마찬가지로 새로운 배열을 선언하고 복사해야 한다.
따라서 시간복잡도는 또 O(n)

자 정리해 보자면
| 마지막에 값 | i번째에 값 | 처음에 값 | ||||
| 인덱스가 i인 원소 접근 | 삽입 | 삭제 | 삽입 | 삭제 | 삽입 | 삭제 |
| O(1) | O(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
2. Dynamic Array
동적배열은 정적 배열과는 다르게 필요에 따라서 크기를 바꿀 수 있는 배열이다. c++에서 vector python 에서 list 등이 이 동적 배열이다. 즉 마지막에 원소를 추가하는 등의 연산을 할 때 정적 배열처럼 새로운 배열을 선언해서 복사할 필요가 없다는 뜻이다.
길이 n의 정적 배열을 선언했을 때는 정확하게 n개를 할당 했었다. 하지만 동적 배열에서는 조금 더 많이 할당한다. (예를 들어 2n개) 또한 자리가 모자라 진다면 다시 상수 배의 크기의 배열을 할당 하여 여유 공간을 만든다. 그렇기 때문에 마지막 원소 뒤에도 남는 공간이 생기게 된다. 그리고 우리는 첫 번째 원소의 주소, 배열 전체의 크기(size), 실제 원소 개수(length) 3가지를 알게 된다.
동적 배열을 이용한 위 4가지의 구현 방법과 시간복잡도를 알아보자.
① 인덱스가 i인 원소에 접근
우리가 배열의 첫 번째 원소의 주소를 알고 있으니 i번째 원소에 접근하기 위해서는
첫 번째 소의 주소 + (자료형 크기)*i 한 주소에 접근하면 된다
따라서 시간 복잡도는 O(1)
② 마지막에 값 삽입, 삭제
정적 배열과 다르게 이제는 맨 뒤에 공간이 남기 때문에 새로운 값을 바로 삽입 할 수 있기 때문에 O(1)의 시간복잡도 일 것 같다.
그런데 뒤에 남은 공간이 없어지면 어떻게 할까? 그렇게 된다면 정적 배열에서처럼 더 큰 배열을 선언해서 배열을 복사해야 할 것이다. 자리가 모자를 때 마다 현재 크기의 2배의 배열을 선언하여 복사한다고 가정하자. 처음 배열을 선언하고 n개의 소를 마지막에 삽입 할 때의 시간복잡도를 계산해 보자.

길이가 0인 배열에
총 1개를 삽입하려면 길이 1의 배열을 선언하여야 한다. ------------ 시간 0 (복사하는 연산 수만 고려)
총 2개를 삽입하려면 위 단계를 거친 후 길이 2의 배열을 선언하고 복사해야 한다. ---- 시간 0 + 1
총 4개를 삽입하려면 위 두 단계를 거친 후 길이 4의 배열을 선언하고 복사해야 한다. - 시간 0 + 1 + 2
총 8개를 삽입하려면 위 세 단계를 거친 후 길이 8의 배열을 선언하고 복사해야 한다. - 시간 0 + 1 + 2 + 4
총 n개를 삽입하려면 위 log_2 n개의 단계를 거친 후 길이 n의 배열을 선언하고 복사해야 한다.
시간 0+1+2+4+8 +... +n 즉 $ O(\sum_{i=0}^{\log_{2}n} 2^i) $이다.
수행시간은 가장 높은 차수의 항에 지배 되므로 위는 $ O(2^{\log_{2}n}) = O(n) $와 같다고 할 수 있다.
따라서 n개의 원소를 삽입하는데 O(n)의 시간 복잡도가 걸리므로 하나의 원소를 삽입하는 데에는 평균O(1)의 시간복잡도를 가진다는 것을 알 수 있다.
③ i번째에 값 삽입, 삭제
삽입하는 공간을 확보하기 위하여 삽입 위치 뒤의 모든 원소를 뒤로 한 칸씩 옮겨야 하고 배열 맨 뒤에 원소를 추가하는 데에는 상수 시간이 걸리므로
시간 복잡도는 O(n)
④ 처음에 값 삽입, 삭제
이것도 마찬가지로 맨 앞의 자리를 확보하기 위하여 뒤의 모든 원소를 뒤로 한 칸씩 옮겨야 하므로
시간복잡도는 O(n)
자 정리해 보자면
| 마지막에 값 | i번째에 값 | 처음에 값 | ||||
| 인덱스가 i인 원소 접근 | 삽입 | 삭제 | 삽입 | 삭제 | 삽입 | 삭제 |
| O(1) | O(1) | O(1) | O(n) | O(n) | O(n) | O(n) |
3. Linked List
두 가지 배열을 모두 알아보았다 배열과 비슷한 자료구조 중에 리스트라는 것에 대해서 추가로 알아보자.
연결리스트는 각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 자료구조이다.

① i번째 원소에 접근
배열처럼 각 원소가 메모리상에서 바로 옆에 있지 않기 때문에 i번째 원소의 주소는 i-1번째 원소를 통해서만 알 수 있다. 따라서 i번째 원소에 접근하기 위해서는 첫번째 원소부터 차례대로 접근해야 한다.
시간복잡도는 O(n)

② 마지막에 값 삽입, 삭제
배열처럼 메모리상에서 연속해 있을 필요가 없기 때문에 새로운 노드를 하나 선언한 뒤 새로운 노드의 주소를 마지막 원소에 저장하면 마지막에 값을 추가 할 수 있으며 삭제시에는 마지막 노드의 주소를 마지막에서 두번째 노드에서 삭제하면 된다.
시간복잡도 O(1)

③ i번째에 값 삽입, 삭제
연결리스트에서는 i번째에 값을 삽입하거나 삭제하는 것도 상수시간에 가능하다.
새로운 노드에 원래 i번째 노드의 주소를 저장하고 i-1번째 노드에 새로운 노드의 주소를 저장하면 된다.
(절대 순서를 거꾸로 하면 안된다. i-1번째 노드에 새로운 노드의 주소를 저장하는 순간 원래 i번째에 있었던 원소의 주소를 잃어버려 더이상 접근이 불가능 하기 때문이다.)

④ 처음에 값 삽입, 삭제
이것도 마찬가지로 위 방법 대로 맨 앞에 삽입 하면 되므로
시간복잡도는 또 O(1)
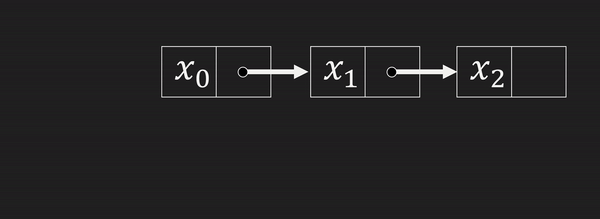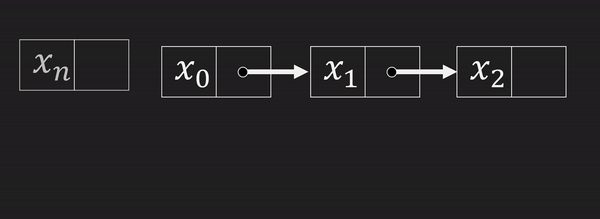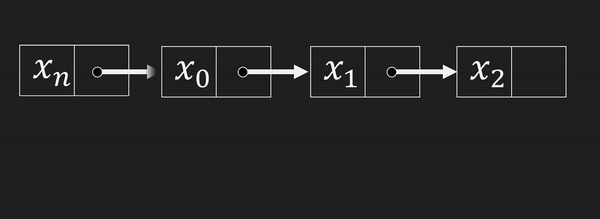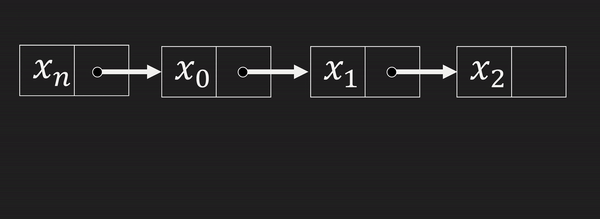
자 정리해 보자면
| 마지막에 값 | i번째에 값 | 처음에 값 | ||||
| 인덱스가 i인 원소 접근 | 삽입 | 삭제 | 삽입 | 삭제 | 삽입 | 삭제 |
| O(1) | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
4. 결론
| 인덱스가 i인 소 접근 | 마지막에 값 삽입,삭제 | i번째에 값 삽입, 삭제 | 처음에 값 삽입, 삭제 | |
| Static Array | O(1) | O(n) | O(n) | O(n) |
| Dynamic Array | O(1) | O(1) | O(n) | O(n) |
| Linked List | O(n) | O(1) | O(1) | O(1) |
동적 배열은 정적배열보다 마지막에 원소를 추가하는데 더 효율 적이고 연결리스트는 배열과는 반대로 중간에 값을 삽입하거나 삭제하는데는 상수시간이 걸리지만 각각의 소에 접근하는데에는 선형시간이 걸리다는 것을 알 수 있었다.
따라서 자료구조의 특징에 맞추어서 적재적소에 잘 사용하는 것이 중요하다.
이렇게 배열에 대해서 알아보았고 연결리스트는 다음에 더 자세히 다뤄보도록 하겠다.
'자료구조 알고리즘' 카테고리의 다른 글
| <자료구조 알고리즘> 그래프 표현 1. adjacency List (인접 리스트) (2) | 2022.02.10 |
|---|---|
| <자료구조 알고리즘> 계획 및 보는 법 (2) | 2022.02.10 |
| <자료구조 알고리즘> 그래프 개념 (0) | 2022.02.10 |
| <자료구조 알고리즘> 정렬 (선택정렬) (0) | 2022.02.09 |
| <자료구조 알고리즘> FFT를 이용한 다항식 곱셈 알고리즘 (0) | 2021.08.15 |


