정렬이란?
선형 자료구조(배열 등)의 원소들을 특정한 순서(오름차순 내림차순등)로 나열하는 것을 이야기 한다. 정렬 자체가 목적일 때도 있겠지만 대부분 검색등의 다른 알고리즘의 전처리 과정으로 사용되는 경우가 많다.
정렬알고리즘 종류
Permutaion Sort, Selection Sort , bubble sort , Quick Sort , Insertion Sort , Merge Sort 등 굉장히 많은 종류의 정렬알고리즘이 있다.
각 알고리즘의 방식과 구현방법, 시간복잡도를 알아보도록 하자.
이 글에서는 오름차순을 기준으로 설명하도록 하겠다.
Bubble sort (버블 정렬)
버블 정렬은 인접한 두 원소의 크기를 비교한는 방법의 정렬알고리즘이다.
배열의 앞에서 부터 두개의 원소의 크기를 비교하여 앞의 더 큰 원소가 뒤쪽에 위치하도록 자리를 바꾼다. 한 단계를 왈료하고 나면 배열의 맨 뒤에 가장 큰 원소 한개가 위치하게 된다. 이를 배열의 길이 만큼 반복해주면 배열을 정렬할 수 있다. ( Selection Sort는 가장 작은 원소 부터 정렬되었지만 bubble sort는 가장 큰 원소 부터 정렬된다.)

687539를 이 방법을 사용해서 같이 한 번 정렬해 보도록 하자.
그림에서 붉은 색은 크기를 비교할 인접한 두 원소이며 초록색은 정렬된 부분이다.
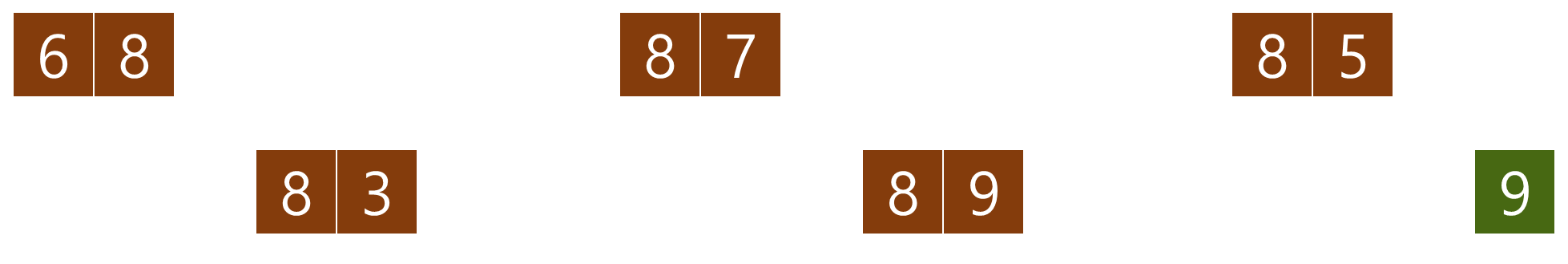
맨 앞 두원소 6, 8을 비교한다. 8이 더 크므로 위치를 바꾸지 않는다.
그 다음 원소 7과 8을 비교한다. 8이 더 크기 때문에 위치를 바꾼다.
8과 5의 크기를 비교한다. 8의 크기가 더 크므로 위치를 바꾼다.
8과 3의 크기를 비교한다. 8의 크기가 더 크므로 위치를 바꾼다.
마지막 9와 8을 비교한다. 9가 더 크므로 위치를 바꾸지 않아도 된다.
가장 큰 원소 9가 마지막에 정렬되었다.
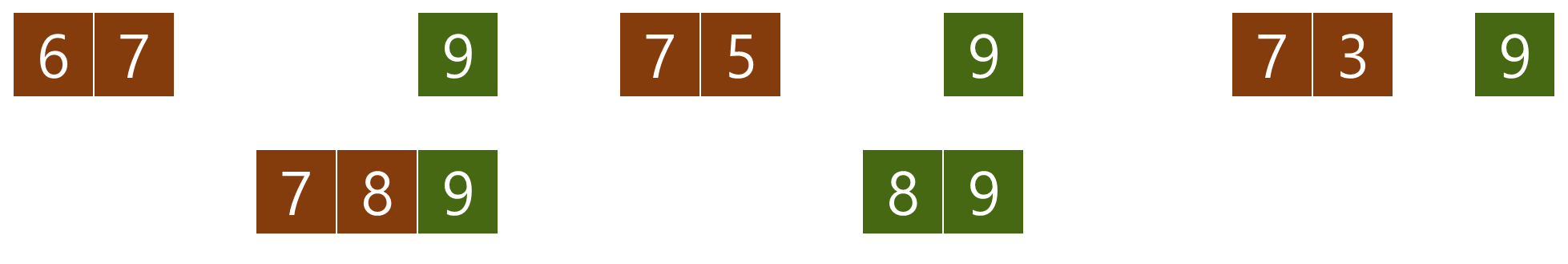
맨 앞 두원소 6, 7을 비교한다. 7이 더 크므로 위치를 바꾸지 않는다.
그 다음 원소 7과 5를 비교한다. 7이 더 크기 때문에 위치를 바꾼다.
7과 3의 크기를 비교한다. 7의 크기가 더 크므로 위치를 바꾼다.
마지막 8과 7을 비교한다. 8이 더 크므로 위치를 바꾸지 않아도 된다.
배열의 끝에 두 원소 8,9가 정렬되었다.

맨 앞 두원소 6, 5을 비교한다. 6이 더 크므로 위치를 바꾼다.
그 다음 원소 6과 3을 비교한다. 6이 더 크기 때문에 위치를 바꾼다.
마지막 6과 7을 비교한다. 7이 더 크므로 위치를 바꾸지 않아도 된다.
배열의 끝에 세 원소 6, 8, 9가 정렬되었다.

맨 앞 두원소 5, 3을 비교한다. 5가 더 크므로 위치를 바꾼다.
마지막 6과 5를 비교한다. 6이 더 크므로 위치를 바꾸지 않아도 된다.
배열의 끝에 네 원소 5, 6, 8, 9가 정렬되었다.

3과 5를 비교한다. 5가 더 크므로 위치를 바꾸지 않아도 된다.
모든 원소 3, 5, 6, 7, 8, 9가 정렬되었다.
시간복잡도
인접 한 두 원소를 비교하는 횟수가 (한 단계마다 정렬되는 배열의 길이가 하나씩 증가하므로) 배열의 길이 -1 부터 단계가 지날 때 마다 1씩 감소한다. 따라서 비교횟수는 $\sum^{n - 1}_{i=1}i = \frac{n(n+1)}{2}$ 이다.
따라서 시간 복잡도는 Selection Sort와 마찬가지로 $O(n^2)$이다. 느리지만 원리가 간단하고 구현이 쉽다는 장점이 있다.

void bubbleSort(vector<int> & v){
int tmp;
for(int i = 0; i < v.size()-1; i++){
for(int j = 1; j < v.size() - i; j++){
if(v[j-1] > v[j]){
tmp = v[j-1];
v[j-1] = v[j];
v[j] = tmp;
}
}
}
}'자료구조 알고리즘' 카테고리의 다른 글
| <자료구조 알고리즘> CCW 알고리즘 (0) | 2022.05.27 |
|---|---|
| <자료구조 알고리즘> 마스터 정리 Master theorem (5) | 2022.05.21 |
| <자료구조 알고리즘> 큐 구현 (0) | 2022.02.22 |
| <자료구조 알고리즘> 큐 (0) | 2022.02.22 |
| <자료구조 알고리즘> 스택 구현 (0) | 2022.02.18 |



